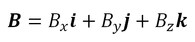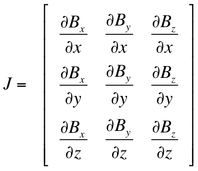Advanced Gradient Analysis
For those more mathematically inclined, the formal definition of the magnetic gradient is expressed as follows. Recall that B is a vector field that has magnitude and direction at each point in space. Using the Cartesian coordinate system with unit vectors i, j, and k along the x-, y- and z-axes, the magnetic field (B) can be expressed as
|
The gradient of B is denoted ∇B, where ∇ is known as the "del" operator. Because B is a vector, ∇B is a Jacobian or 2nd order tensor, a matrix of 9 partial derivatives of the 3 principal components of B (Bx, By, and Bz) with respect to the 3 cardinal directions (x, y, and z).
In other words, the gradient of a vector field like B is a rather complex entity, as you must consider how each component of the field may vary in each direction. |
Jacobian of B
|
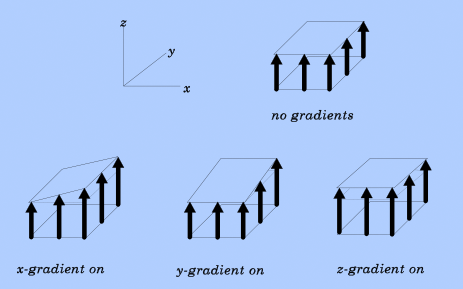
In the simplified example above we have assumed B to be directed purely along the z-axis (i.e., Bx = 0 and By = 0) and without change in the x- or y-directions (i.e., all partial derivatives with respect to x and y are also zero). So, when we stated that the gradient (G) was 2 mT/meter, what we really meant was that the rate of change of z-component of B in the z-direction (∂Bz/∂z) = 2 mT/meter, and that all other terms in the Jacobian were zero.
Fortunately, in MR imaging, we can often assume relatively simplified cases like the one above. For example, the x-, y- and z-gradients used for imaging are generally considered to create variations of B only with respect to the Bz component. Thus as a good first order approximation, we need only consider the partial derivatives in the third column of the Jacobian, assuming all derivatives in the first two columns are zero.
Fortunately, in MR imaging, we can often assume relatively simplified cases like the one above. For example, the x-, y- and z-gradients used for imaging are generally considered to create variations of B only with respect to the Bz component. Thus as a good first order approximation, we need only consider the partial derivatives in the third column of the Jacobian, assuming all derivatives in the first two columns are zero.
Gradients used for imaging can be considered to distort the main field Bo only with respect to the z-direction. The x-gradient, for example, does not "shear" the field horizontally or alter the main direction of Bo, it only makes Bz stronger on one side of the scanner than the other.
References
Elster AD, Burdette JH. Questions and Answers in MRI, 2nd ed. St. Louis: Mosby, 2001, pp 1-3.
"Magnetism." Wikipedia, The Free Encyclopedia (Accessed 1 Aug 2013)
Elster AD, Burdette JH. Questions and Answers in MRI, 2nd ed. St. Louis: Mosby, 2001, pp 1-3.
"Magnetism." Wikipedia, The Free Encyclopedia (Accessed 1 Aug 2013)
Related Questions
What causes magnetism?
What causes magnetism?